【编译】三万字长文！LSTM 之父 Jürgen 带我们回顾深度学习发展史
本文译自 LSTM 作者 Jürgen Schmidhuber, KAUST AII, Swiss AI Lab IDSIA, USI，中文译文由 AI 及麦克船长完成翻译。
本文目录
- 现代人工智能和深度学习的注释历史
- 介绍
- 1676：向后信用分配的链式规则
- ~1800：第一个神经网络/线性回归/浅层学习
- 1920-1925：第一个循环网络架构
- 1958 年：多层前馈神经网络（没有深度学习）
- 1965 年：第一次深度学习
- 1967-68：通过随机梯度下降进行深度学习
- 1970 年：反向传播。 1982 年：对于神经网络。 1960 年：先驱。
- 1979 年：第一个深度卷积神经网络（1969 年：ReLU）
- 1980 年代至 90 年代：图形神经网络/随机增量规则（Dropout）/…
- 1990 年 2 月：生成对抗网络/好奇心
- 1990 年 2 月：生成对抗网络/好奇心
- 1991 年 4 月：通过自监督预训练进行深度学习
- 1991 年 6 月：基本问题：梯度消失
- 1991 年 6 月：LSTM / Highway Nets / ResNets 的根源
- 是硬件，笨蛋！
- 不要忽视 1931 年以来的人工智能理论
- 从大爆炸到遥远的未来的更广泛的历史背景
现代人工智能和深度学习的注释历史
摘要。 机器学习（ML）是信用分配的科学：在观察中发现预测行动后果的模式，并帮助提高未来的表现。信用分配也是人类理解世界如何运作的必要条件，不仅对于每天生活中的个人，而且对于像历史学家这样的学术专业人士来说也是如此。在这里，我主要关注现代人工智能（AI）的历史，它由人工神经网络（NNs）和深度学习（DL）主导，在概念上更接近早期的控制论，而不是自1956年以来被称为 AI（例如专家系统和逻辑编程）的领域。现代AI的历史重点将强调传统AI教科书以外的突破，特别是当今NNs的数学基础，如链式规则（1676 年），第一个NNs（线性回归，约1800年）和第一个工作的深度学习器（1965-）。从2022年的角度来看，我提供了一个时间表，阐述了NNs，深度学习，AI，计算机科学和数学领域中事后看来最重要的相关事件，并对那些奠定了这一领域基础的人进行了赞扬。文章中包含了许多与我的AI博客相关的概述网站的超链接。它还揭示了深度学习的一些流行但是误导性的历史条目，并补充了我之前的深度学习调查[DL1]，其中提供了数百条额外的参考资料。最后，为了结束这篇文章，我将把事情放在更广泛的历史背景中，跨越从大爆炸开始到宇宙将比现在老很多倍的时间。本文也是我即将出版的AI书籍的一章的草稿。
免责声明。 有人说深度学习的历史不应该由帮助塑造它的人来写——“你是历史的一部分，而不是历史学家。”[CONN21] 我不同意这种观点。 由于我似乎比其他人更了解深度学习的历史，[S20][DL3,DL3a][T22][DL1-2] 我认为记录和推广这些知识是我的责任，即使这似乎暗示着与 兴趣，因为这意味着突出提及我自己团队的工作，因为（截至 2022 年）引用最多的神经网络都是基于它的。[MOST] 未来的人工智能历史学家可能会纠正任何时代特定的潜在偏见。
介绍
随着时间的推移，某些历史事件在某些旁观者眼中变得更加重要。 例如，138 亿年前的大爆炸现在被广泛认为是万物历史上的重要时刻。 然而，直到几十年前，地球人还完全不知道它，长期以来，地球人对宇宙的起源抱有相当错误的看法（有关世界历史的更多信息，请参见最后一节）。 目前接受的许多更有限主题的历史是类似激进修订的结果。 在这里，我将重点关注人工智能 (AI) 的历史，它也与过去不同。
1980 年代写的 AI 历史会强调定理证明、[GOD][GOD34][ZU48][NS56] 逻辑编程、专家系统和启发式搜索等主题。[FEI63,83][LEN83] 这将是 与 1956 年达特茅斯会议的主题一致，约翰麦卡锡在会上创造了“人工智能”一词，用来描述一个旧的研究领域重新引起人们的兴趣。 实用 AI 至少可以追溯到 1914 年，当时 Leonardo Torres y Quevedo（见下文）构建了第一个工作的国际象棋终端游戏玩家 [BRU1-4]（当时国际象棋被认为是一种仅限于智能生物领域的活动）。 AI 理论至少可以追溯到 1931-34 年，当时 Kurt Gödel（见下文）确定了任何类型的基于计算的 AI 的基本限制。[GOD][BIB3][GOD21,a,b]
2000 年代初期编写的 AI 历史会更加强调支持向量机和内核方法等主题，[SVM1-4] 贝叶斯（实际上是拉普拉斯或可能是桑德森[STI83-85]）推理[BAY1-8][ FI22]和其他概率论和统计概念，[MM1-5][NIL98][RUS95]决策树，例如[MIT97]集成方法，[ENS1-4]群体智能，[SW1]和进化计算。EVO1 -7为什么？ 因为在当时，此类技术推动了许多成功的 AI 应用。
写于 2020 年代的 AI 历史必须强调诸如更古老的链式法则 [LEI07] 和通过梯度下降训练的深度非线性人工神经网络 (NN) [GD’] 等概念，特别是基于反馈的循环网络，它们是 其程序是权重矩阵的通用计算机。[AC90] 为什么？ 因为最近许多最著名和最商业化的 AI 应用程序都依赖于它们。[DL4]
这样的 NN 概念实际上在概念上接近 MACY 会议 (1946-1953)[MACY51] 和 1951 年关于计算机器和人类思想的巴黎会议的主题，现在通常被视为关于 AI 的第一次会议。[AI51][BRO21][ BRU4] 然而，在 1956 年之前，现在称为 AI 的大部分内容仍被称为控制论，重点与基于神经网络“深度学习”的现代 AI 非常一致。[DL1-2][DEC]
过去的一些神经网络研究受到人脑的启发，人脑有大约 1000 亿个神经元，每个神经元平均连接到 10,000 个其他神经元。 有些是输入神经元，为其余神经元提供数据（声音、视觉、触觉、疼痛、饥饿）。 其他的是控制肌肉的输出神经元。 大多数神经元隐藏在两者之间，思考发生的地方。 你的大脑显然通过改变连接的强度或权重来学习，这决定了神经元相互影响的强度，并且似乎编码了你一生的所有经历。 与我们的人工 NN 类似，它比以前的方法学习得更好，可以识别语音或手写或视频、最小化痛苦、最大化快乐、驾驶汽车等。[MIR]（第 0 节）[DL1-4]
NN 如何学习所有这些？ 在下文中，我将强调使这一切成为可能的重要历史贡献。 由于现代 AI 的几乎所有基本概念都源于前几千年，因此下面的章节标题只强调到 2000 年的发展。然而，许多章节都提到了这项工作在新千年的后期影响，这带来了许多 硬件和软件的改进，有点像 20 世纪对 19 世纪发明的汽车进行了大量改进。
本文还揭穿了一个经常重复的、误导性的“深度学习的历史”[S20][DL3,3a]，它忽略了下面提到的大部分开创性工作。[T22]见脚注 6。本文的标题图片是一个 对一条错误的常识的反应，该常识说 [T19] 使用神经网络“作为帮助计算机识别模式和模拟人类智能的工具是在 1980 年代引入的”，尽管这种神经网络早在 1980 年代就出现了。 [T22 ] 确保在所有科学中正确分配学分对我来说非常重要——就像对所有科学家一样——我鼓励有兴趣的读者也看看我在《科学》和《自然》杂志上就此发表的一些信件，例如， 关于航空史，[NASC1-2] 电话，[NASC3] 计算机，[NASC4-7] 弹性机器人，[NASC8] 和 19 世纪的科学家。[NASC9]
最后，为了圆满结束，我将把事情放在更广泛的历史背景下，跨越从大爆炸到宇宙比现在古老许多倍的时间。
1676：向后信用分配的链式规则
莱布尼茨，大约 1670 年的计算机科学之父，于 1676 年发表了链式法则
1676年，戈特弗里德·威廉·莱布尼茨在回忆录中发表了微积分的链式法则（尽管万物皆有符号错误！）； Guillaume de l’Hopital 在他 1696 年关于莱布尼茨微积分的教科书中对此进行了描述。[LEI07-10][L84] 今天，这条规则是深度神经网络 (NN) 中信用分配的核心。 为什么？ 最流行的 NN 具有计算来自其他神经元的输入的可微函数的节点或神经元，这些节点或神经元又计算来自其他神经元的输入的可微函数，等等。 问题是：如果我们稍微修改早期函数的参数或权重，最终函数的输出将如何变化？ 链式法则是计算答案的基本工具。
Cauchy 这个答案被梯度下降 (GD) 技术使用，显然是由 Augustin-Louis Cauchy 于 1847 年首次提出 [GD’]（后来由 Jacques Hadamard [GD’’] 提出；称为 SGD 的随机版本归功于 Herbert 罗宾斯和萨顿门罗 (1951)[STO51-52])。 为了教会神经网络将来自训练集的输入模式转换为所需的输出模式，所有神经网络权重都朝着最大局部改进的方向迭代改变一点，以创建稍微更好的神经网络，依此类推，直到获得令人满意的解决方案 成立。
脚注 1. 1684 年，莱布尼茨也是第一个发表“现代”微积分的人；[L84][SON18][MAD05][LEI21,a,b] 后来艾萨克·牛顿也因其未发表的工作而受到赞誉。[SON18] 他们的优先事项 然而，争议 [SON18] 并不包含链式法则。[LEI07-10] 当然，两者都建立在早期工作的基础上：在公元前 2 世纪，阿基米德（也许是有史以来最伟大的科学家 [ARC06]）为 无穷小并发表了微积分的特例，例如球体和抛物线段，建立在古希腊更早的工作之上。 14 世纪，Sangamagrama 的 Madhava 和印度喀拉拉邦学派的同事也进行了微积分的基础工作。[MAD86-05]
脚注 2. 值得注意的是，莱布尼茨（1646-1714 年，又名“世界上第一位计算机科学家”[LA14]）也奠定了现代计算机科学的基础。 他设计了第一台可以执行所有四种算术运算的机器（1673），以及第一台带有内部存储器的机器。[BL16] 他描述了二进制计算机的原理（1679）[L79][L03][LA14][HO66][ LEI21,a,b] 几乎被所有现代机器所采用。 他的正式思想代数 (1686)[L86][WI48] 与后来的布尔代数 (1847) 演绎等价[LE18]。[BOO] 他的 Characteristica Universalis & Calculus Ratiocinator 旨在通过计算回答所有可能的问题；[WI48 】 他的《微积分！ 是启蒙时代的标志性名言之一。 值得注意的是，他还负责链式法则，这是“现代”深度学习的基础，是现代计算机科学的一个重要子领域。
脚注 3. 有人声称反向传播算法（进一步讨论；现在广泛用于训练深度神经网络）只是 Leibniz (1676) & L’Hopital (1696) 的链式法则。[CONN21] 不，这是有效的方法 将链式法则应用于具有可微分节点的大型网络（也有许多低效的方法）。[T22] 直到 1970 年才发布，如下所述。[BP1,4,5]
~1800：第一个神经网络/线性回归/浅层学习
1805 年，Adrien-Marie Legendre 发表了现在通常称为线性神经网络 (NN) 的内容。 约翰·卡尔·弗里德里希·高斯 (Johann Carl Friedrich Gauss) 也因在大约 1795 年完成的早期未发表的工作而受到赞誉
1805 年，Adrien-Marie Legendre 发表了现在通常称为线性神经网络 (NN) 的内容。 后来，约翰·卡尔·弗里德里希·高斯 (Johann Carl Friedrich Gauss) 也因在大约 1795 年完成的这项未发表的工作而受到赞誉。[STI81]
这个来自 2 个多世纪前的神经网络有两层：一个具有多个输入单元的输入层和一个输出层。 为简单起见，我们假设后者由单个输出单元组成。 每个输入单元都可以保存一个实数值，并通过具有实数值权重的连接连接到输出。 NN 的输出是输入与其权重的乘积之和。 给定输入向量的训练集和每个向量的期望目标值，调整 NN 权重，使 NN 输出与相应目标之间的平方误差之和最小化。
1795 年，高斯使用了现在称为线性神经网络的东西，但勒让德于 1805 年首次发表了它。高斯通常被称为自古以来最伟大的数学家，当然，那时候还不叫神经网络。 它被称为最小二乘法，也被广泛称为线性回归。 但它在数学上与今天的线性神经网络相同：相同的基本算法、相同的误差函数、相同的自适应参数/权重。 这种简单的神经网络执行“浅层学习”（与具有许多非线性层的“深度学习”相反）。 事实上，许多神经网络课程都是从介绍这种方法开始的，然后转向更复杂、更深入的神经网络。
也许第一个通过浅层学习进行模式识别的著名例子可以追溯到 200 多年前：1801 年通过高斯重新发现矮行星谷神星，他从以前的天文观测中获得了数据点，然后使用各种技巧来调整模型的参数 预测器，它基本上学会了从训练数据中进行归纳以正确预测谷神星的新位置。
脚注 4. 今天，所有技术学科的学生都必须上数学课，尤其是分析、线性代数和统计学。 在所有这些领域中，重要的结果和方法（至少部分）归功于高斯：代数基本定理、高斯消去法、统计的高斯分布等。这位号称“自古以来最伟大的数学家”的人也开创了微分 几何、数论（他最喜欢的科目）和非欧几何。 此外，他对天文学和物理学做出了重大贡献。 如果没有他的成果，包括 AI 在内的现代工程将不可想象。
脚注 5. 神经网络的“浅层学习”在 1950 年代后期经历了新一波的流行。 Rosenblatt 的感知器 (1958)[R58] 将上述线性 NN 与输出阈值函数相结合以获得模式分类器（比较他在下面讨论的多层网络上更先进的工作）。 Joseph[R61] 提到了 Farley & Clark 更早的类似感知器的设备。 Widrow & Hoff 的类似 Adaline 在 1962 年学到。[WID62]
1920-1925：第一个循环网络架构
1924 年，Ernst Ising 发表了第一个循环网络架构：Ising 模型或 Lenz-Ising 模型。 与人脑相似，但与更有限的前馈神经网络 (FNN) 不同，循环神经网络 (RNN) 具有反馈连接，因此可以遵循从某些内部节点到其他节点的定向连接，并最终在起点处结束。 这对于在序列处理期间实现对过去事件的记忆是必不可少的。
第一个非学习 RNN 架构（Ising 模型或 Lenz-Ising 模型）是由物理学家 Ernst Ising 和 Wilhelm Lenz 在 1920 年代引入和分析的[L20][I24,I25][K41][W45][T22] 它 响应输入条件进入平衡状态，并且是第一个学习 RNN 的基础（见下文）。
非学习 RNN 也在 1943 年由神经科学家 Warren McCulloch 和 Walter Pitts [MC43] 进行了讨论，并在 1956 年由 Stephen Cole Kleene 进行了正式分析。 [K56]
1972 年，Shun-Ichi Amari 使 Ising 递归网络自适应。 这是第一个发表的学习人工递归神经网络
~1972：首次发布学习人工 RNN
1972 年，Shun-Ichi Amari 使 Lenz-Ising 循环架构具有自适应性，这样它就可以通过改变连接权重来学习将输入模式与输出模式相关联。[AMH1] 另见 Stephen Grossberg 关于生物网络的工作，[GRO69] David Marr 的 [MAR71]和Teuvo Kohonen的[KOH72]工作，以及Kaoru Nakano的学习RNN。[NAK72]
艾伦·图灵 10 年后，Amari 网络被重新发布（并分析了它的存储容量）。[AMH2] 有人称它为 Hopfield 网络（！）或 Amari-Hopfield 网络。[AMH3] 它不处理序列，但在响应中达到平衡 到静态输入模式。 然而，Amari (1972) 也对其进行了序列处理推广[AMH1]
值得注意的是，早在 1948 年，艾伦图灵就提出了与人工进化和学习 RNN 相关的想法。 然而，这在几十年后首次发表，[TUR1] 这解释了他在这里思想的晦涩。[TUR21]（边注：有人指出，著名的“图灵测试”实际上应该称为“笛卡尔测试” .[TUR3,a,b][TUR21])
今天最流行的RNN就是下面提到的长短期记忆（LSTM），它已经成为20世纪被引用最多的NN[MOST]
1958 年：多层前馈神经网络（没有深度学习）
1958 年，弗兰克·罗森布拉特 (Frank Rosenblatt) 拥有多层感知器，其最后一层学习
1958 年，Frank Rosenblatt 不仅结合了线性 NN 和阈值函数（参见 1800 年以来的浅层学习部分），他还有更有趣、更深层的多层感知器 (MLP)。[R58] 他的 MLP 有一个非学习的第一层 随机权重和自适应输出层。 虽然这还不是深度学习，因为只有最后一层学习了，[DL1] Rosenblatt 基本上拥有了后来被重新命名为极限学习机 (ELM) 的东西，但没有适当的归因。[ELM1-2][CONN21][T22]
1961 年，Karl Steinbuch [ST61-95] 和 Roger David Joseph [R61] (1961) 也讨论了 MLP。 另见 Oliver Selfridge 的多层 Pandemonium [SE59] (1959)。
Rosenblatt (1962) 甚至写了关于带有隐藏层的 MLP 中的“反向传播错误”[R62]，尽管他还没有针对深度 MLP 的通用深度学习算法。 现在称为反向传播的东西完全不同，它于 1970 年首次发布，如下所述。[BP1-BP5][BPA-C]
今天，最流行的 FNN 是基于 LSTM 的 Highway Net（下文提到）的一个版本，称为 ResNet，[HW1-3]，它已成为 21 世纪被引用最多的 NN。[MOST]
1965 年：第一次深度学习
1965 年，Alexey Ivakhnenko 和 Valentin Lapa 推出了第一个适用于具有任意多个隐藏层的深度 MLP 的深度学习算法 深度前馈网络架构的成功学习始于 1965 年的乌克兰（当时的苏联），当时 Alexey Ivakhnenko 和 Valentin Lapa 为具有任意多个隐藏层（已经包含现在流行的乘法门）的深度 MLP 引入了第一个通用的工作学习算法 .[DEEP1-2][DL1-2][FDL] 1971年的一篇论文[DEEP2]已经描述了一个8层的深度学习网络，用他们被高度引用的方法训练，这种方法在新千年仍然很流行，[DL2]尤其是 在东欧，那里诞生了很多机器学习。[MIR]（第 1 节）[R8]
给定一组具有相应目标输出向量的输入向量训练集，层逐渐增长并通过回归分析进行训练，然后借助单独的验证集进行修剪，其中正则化用于清除多余的单元。 层数和每层单元以问题相关的方式学习。
与后来的深度神经网络一样，Ivakhnenko 的网络学会了为传入数据创建分层的、分布式的、内部表示。
他没有称它们为深度学习神经网络，但它们就是这样。 事实上，“深度学习”这个古老的术语最早是由 Dechter (1986) 引入机器学习的，Aizenberg 等人 (2000) 引入神经网络的。[DL2]（边注：我们 2005 年关于深度学习的论文 [DL6 ,6a] 是第一本机器学习出版物，标题中包含“深入学习”这个词组合。[T22])
1967-68：通过随机梯度下降进行深度学习
1967-68 年，Shun-Ichi Amari 通过随机梯度下降训练深度 MLP Ivakhnenko 和 Lapa（1965 年，见上文）逐层训练他们的深层网络。 然而，在 1967 年，Shun-Ichi Amari 建议通过随机梯度下降 (SGD)[GD1] 从头开始以非增量端到端方式训练多层 MLP，这是 Robbins 和 Monro 于 1951 年提出的一种方法。 STO51-52]
Amari 的实现 [GD2,GD2a]（与他的学生 Saito）在具有两个可修改层的五层 MLP 中学习了内部表示，该层被训练为对非线性可分离模式类进行分类。 那时候的计算成本是今天的数十亿倍。
另见 Iakov Zalmanovich Tsypkin 更早的关于非线性系统的基于梯度下降的在线学习的工作。[GDa-b]
值得注意的是，如上所述，Amari 还在 1972 年发表了学习 RNN。[AMH1]
1970 年：反向传播。 1982 年：对于神经网络。 1960 年：先驱。
谁发明了反向传播？
1970 年，Seppo Linnainmaa 是第一个发布现在称为反向传播的算法，这是一种著名的可微节点网络信用分配算法，[BP1,4,5] 也称为“自动微分的反向模式”。 它现在是广泛使用的神经网络软件包的基础，例如 PyTorch 和谷歌的 Tensorflow。
1960年，Henry J. Kelley在控制理论领域有了反向传播的先驱 1982 年，Paul Werbos 在他 1974 年的论文中提出了使用该方法训练神经网络，[BP2] 扩展了思想。
1960 年，Henry J. Kelley 在控制理论领域已经有了反向传播的先驱；[BPA] 另请参阅 Stuart Dreyfus 和 Arthur E. Bryson 在 1960 年代早期的后期工作。[BPB][BPC][R7] 不同于 Linnainmaa 的一般方法，[BP1] 1960 年代的系统[BPA-C] 通过标准雅可比矩阵计算从一个“阶段”到前一个“阶段”反向传播导数信息，既没有解决跨多个阶段的直接链接，也没有解决由于网络导致的潜在额外效率增益 稀疏性。
反向传播本质上是为深度网络实施莱布尼茨链式法则 [LEI07-10] (1676)（见上文）的有效方式。 Cauchy 的梯度下降 [GD’] 使用它在许多试验过程中逐渐削弱某些 NN 连接并加强其他连接，这样 NN 的行为越来越像某个老师，可能是一个人，也可能是另一个 NN，[UN- UN2] 或其他东西。
到 1985 年，计算成本已比 1970 年便宜约 1,000 倍，而第一台台式计算机刚刚在富裕的学术实验室中普及。 David E. Rumelhart 等人对已知方法[BP1-2] 的实验分析。 然后证明反向传播可以在 NN 的隐藏层中产生有用的内部表示。[RUM] 至少对于监督学习，反向传播通常比 Amari 的上述深度学习更有效，通过更一般的 SGD 方法（1967），它学习了有用的内部 大约 2 年前 NN 中的表示。[GD1-2a]
直到 1970 年 [BP1-2] 的反向传播方法被广泛接受作为深度神经网络的训练方法，花了 4 年时间。 在 2010 年之前，许多人认为训练多层神经网络需要无监督预训练，这是我自己在 1991 年提出的方法[UN][UN0-3]（见下文），后来得到其他人的支持（2006 年）。[UN4 ] 事实上，据称 [VID1] “没有任何头脑正常的人会建议”将简单的反向传播应用于深度神经网络。 然而，在 2010 年，我们的团队与我出色的罗马尼亚博士后 Dan Ciresan [MLP1-2] 表明，深度 FNN 可以通过简单的反向传播进行训练，并且根本不需要对重要应用进行无监督预训练。 [MLP2]
我们的系统在当时著名且广泛使用的图像识别基准 MNIST 上创造了新的性能记录 [MLP1]。 这是通过在称为 GPU 的高度并行图形处理单元上极大地加速深度 FNN 来实现的（正如 Jung 和 Oh 在 2004 年 [GPUNN] 首次对层数较少的浅层 NN 所做的那样）。 一位评论家称这是“机器学习社区的警钟”。 今天，该领域的每个人都在追求这种方法。
脚注 6. 不幸的是，在 1980 年代重新发表反向传播的几位作者没有引用现有技术——甚至在后来的调查中也没有。[T22] 事实上，正如引言中提到的，有一个更广泛的、经常重复的、误导性的“ 深度学习的历史[S20]忽略了前面章节中提到的大部分开创性工作。[T22][DLC]这个“替代历史”基本上是这样的：“1969 年，Minsky & Papert[M69] 表明浅 没有隐藏层的神经网络非常有限，该领域被放弃，直到新一代神经网络研究人员在 1980 年代重新审视这个问题。[S20] 然而，1969 年的书 [M69] 解决了高斯的“问题” & Legendre 的浅层学习（大约 1800 年）[DL1-2] 已经在 4 年前被 Ivakhnenko & Lapa 流行的深度学习方法 [DEEP1-2][DL2] 解决了，然后 Amari 的 SGD 也解决了 MLPs。[GD1- 2] Minsky 既没有引用这项工作，也没有在后来更正他的书。HIN[T22] 甚至 r 最近的论文宣扬了这种对深度学习的修正主义叙述，显然是为了美化其作者后来的贡献（例如玻尔兹曼机[BM][HIN][SK75][G63][T22]），而没有将它们与原始作品联系起来，[DLC ][S20][T22]虽然真实历史众所周知。 深度学习研究在 1960 年代至 70 年代非常活跃，尤其是在英语圈之外。[DEEP1-2][GD1-3][CNN1][DL1-2][T22] 明显的错误归因和无意的[PLAG1][CONN21] 或故意 [FAKE2] 剽窃仍在污染整个深度学习领域。[T22] 科学期刊“需要对自我纠正做出更明确、更坚定的承诺”，[SV20] 这已经是其他科学领域的标准。
1979 年：第一个深度卷积神经网络（1969 年：ReLU）
1979 年，Kunihiko Fukushima 引入了卷积神经网络 (CNN) 架构。计算机视觉在 2010 年代被称为卷积神经网络 (CNN) 的特殊前馈神经网络彻底改变了。[CNN1-4] 具有交替卷积层和下采样层的基本 CNN 架构 这要归功于福岛邦彦 (1979)。 他称之为 Neocognitron。[CNN1]
值得注意的是，早在 10 年前，Fukushima 还为神经网络引入了整流线性单元 (ReLU) (1969)。[RELU1] 它们现在广泛用于 CNN 和其他神经网络。
1987 年，Alex Waibel 将带卷积的神经网络与权重共享和反向传播相结合（见上文），[BP1-2] 并将其应用于语音。[CNN1a] Waibel 没有称此为 CNN，而是 TDNN。
Yamaguchi 等人介绍了一种流行的下采样变体，称为最大池化。 1990 年的 TDNN [CNN3a] 和 Juan Weng 等人。 1993 年用于高维 CNN。[CNN3]
自 1989 年以来，Yann LeCun 的团队为 CNN 的改进做出了贡献，尤其是在图像方面。[CNN2,4][T22] Baldi 和 Chauvin (1993) 首次将具有反向传播功能的 CNN 应用于生物医学/生物特征图像。[BA93]
2011 年晚些时候，CNN 在 ML 社区变得更加流行，当时我自己的团队大大加快了深度 CNN 的训练（Dan Ciresan 等人，2011）。[GPUCNN1,3,5] 我们基于 GPU 的快速 [GPUNN][ GPUCNN5] 2011 年的 CNN [GPUCNN1] 被称为 DanNet[DAN,DAN1][R6] 是一个实际的突破，比 2006 年早期的 GPU 加速 CNN 更深更快。[GPUCNN] 2011 年，DanNet 成为第一个纯深度 CNN 赢得计算机视觉竞赛。[GPUCNN2-3,5]
| Competition[GPUCNN5] | Date/Deadline | Image size | Improvement | Winner |
|---|---|---|---|---|
| IJCNN 2011 traffic signs | Aug 06, 2011 | variable | 68.0% (superhuman) | DanNet[DAN,DAN1] |
| ISBI 2012 image segmentation | Mar 01, 2012 | 512x512 | 26.1% | DanNet[GPUCNN3a] |
| ICPR 2012 medical imaging | Sep 10, 2012 | 2048x2048x3 | 8.9% | DanNet[GPUCNN3a] |
| ImageNet 2012 | Sep 30, 2012 | 256x256x3 | 41.4% | AlexNet[GPUCNN4] |
| MICCAI 2013 Grand Challenge | Sep 08, 2013 | 2048x2048x3 | 26.5% | DanNet[GPUCNN8] |
| ImageNet 2014 | Aug 18, 2014 | 256x256x3 | 15.8% | VGG Net[GPUCNN9] |
| ImageNet 2015 | Sep 30, 2015 | 256x256x | 315.8% | ResNet,[HW2] a Highway Net[HW1] with open gates |
有一段时间，DanNet 享有垄断地位。 从 2011 年到 2012 年，它赢得了它参加的所有比赛，并连续赢得了四场比赛（2011 年 5 月 15 日、2011 年 8 月 6 日、2012 年 3 月 1 日、2012 年 9 月 10 日）。[GPUCNN5] 特别是在硅谷的 IJCNN 2011 上，DanNet 吹响了比赛，并在国际比赛中取得了第一个超人视觉模式识别[DAN1]。 DanNet 也是第一个获胜的深度 CNN：中国手写比赛（ICDAR 2011）、图像分割比赛（ISBI，2012 年 5 月）、大图像物体检测比赛（ICPR，2012 年 9 月 10 日），以及——在 同一时间——关于癌症检测的医学成像竞赛。[GPUCNN8] 2010 年，我们将 DanNet 介绍给世界上最大的钢铁生产商 Arcelor Mittal，并且能够大大提高钢铁缺陷检测。[ST] 据我所知， 这是重工业的第一个深度学习突破。 2012 年 7 月，我们关于 DanNet[GPUCNN3] 的 CVPR 论文引起了计算机视觉社区的注意。 5 个月后，类似的 GPU 加速 AlexNet 赢得了 ImageNet[IM09] 2012 竞赛。[GPUCNN4-5][R6] 我们的 CNN 图像扫描仪比以前的方法快 1000 倍。[SCAN] 这引起了医疗保健行业的极大兴趣 . 今天，IBM、西门子、谷歌和许多初创公司都在采用这种方法。 VGG 网络（ImageNet 2014 获胜者）[GPUCNN9] 和其他高引用的 CNNs[RCNN1-3] 进一步扩展了 2011 年的 DanNet。[MIR]（第 19 节）[MOST]
ResNet，ImageNet 2015 的赢家[HW2]（2015 年 12 月）和目前被引用最多的神经网络，[MOST] 是我们早期 Highway Net（2015 年 5 月）的一个版本（开门）[HW1-3][R5] Highway Net（见下文）实际上是我们的 vanilla LSTM（见下文）的前馈网络版本。[LSTM2] 它是第一个有效的、真正具有数百层的深度前馈神经网络（以前的神经网络最多只有几十层） .
1980 年代至 90 年代：图形神经网络/随机增量规则（Dropout）/…
v.d. 引入了具有快速变化的“快速权重”的神经网络。 Malsburg (1981) 等人。[FAST,a,b] 1987 年由 Pollack [PO87-90] 提出并由 Sperduti、Goller 和 Küchler 扩展/改进的可以操纵图形等结构化数据的深度学习架构 [T22] 在 1990 年代初期。[SP93-97][GOL][KU][T22] 另见我们的图 NN-like, Transformer-like Fast Weight Programmers of 1991[FWP0-1][FWP6][FWP] 学习不断 重写从输入到输出的映射（见下文），以及 Baldi 及其同事的工作。[BA96-03] 如今，图 NN 用于许多应用程序。
Werbos,[BP2][BPTT1] Williams,[BPTT2][CUB0-2]等人[ROB87][BPTT3][DL1]分析了梯度下降的实现方式[GD’][STO51-52][GDa-b][ GD1-2a] 在 RNN 中。 Kohonen 的自组织映射开始流行。[KOH82-89]
80 年代和 90 年代还看到了各种生物学上更合理的深度学习算法的提议，与反向传播不同，这些算法在空间和时间上是局部的。[BB2][NAN1-4][NHE][HEL] 参见概述[MIR]（第 15 节） ，第 17 节）以及最近对此类方法重新产生的兴趣。[NAN5][FWPMETA6][HIN22]
1990 年，Hanson 引入了随机增量法则，这是一种通过反向传播训练神经网络的随机方法。 几十年后，这个版本在绰号“dropout”下流行起来。[Drop1-4][GPUCNN4]
1980 年代和 90 年代发表了许多关于 NN（包括 RNN）的其他论文——请参阅 2015 年调查中的大量参考文献。[DL1] 然而，在这里，我们主要将自己限制在——事后看来——最重要的论文，鉴于目前 （短暂的？）2022 年的前景。
1990 年 2 月：生成对抗网络/好奇心
生成对抗网络 (GAN) 已经变得非常流行。[MOST] 它们于 1990 年首次在慕尼黑以人工好奇心的名义发表。[AC90-20][GAN1] 两个决斗的神经网络（一个概率生成器和一个预测器）正试图 在 minimax 游戏中最大化彼此的损失。[AC]（第 1 节）生成器（称为控制器）生成概率输出（使用随机单位 [AC90]，就像在后来的 StyleGANs[GAN2] 中一样）。 预测器（称为世界模型）看到控制器的输出并预测环境对它们的反应。 使用梯度下降，预测器 NN 最小化它的错误，而生成器 NN 试图使输出最大化这个错误：一个网络的损失是另一个网络的收益。[AC90]（世界模型也可以用于连续在线行动规划。 [AC90][计划 2-3][计划])
在 2014 年一篇关于 GAN 的论文之前 4 年，[GAN1] 我著名的 2010 年调查 [AC10] 将 1990 年的生成对抗性神经网络总结如下：“神经网络作为预测世界模型用于最大化控制器的内在奖励，这 与模型的预测误差成正比”（已最小化）。
2014 年的 GAN 就是这样的一个例子，其中试验非常短（就像老虎机问题）并且环境简单地返回 1 或 0，这取决于控制器（或生成器）的输出是否在给定的集合中。[AC20][AC] [T22]（第十七节）
其他早期的对抗性机器学习设置 [S59][H90] 非常不同——它们既不涉及无监督神经网络，也不涉及建模数据，也不使用梯度下降。[AC20]
可预测性最小化：无监督极小极大博弈，其中一个神经网络最小化另一个最大化的目标函数
1990 年的原则已被广泛用于强化学习 [SIN5][OUD13][PAT17][BUR18] 和逼真图像合成 [GAN1,2] 的探索，尽管后者最近被 Rombach 等人接管。 s Latent Diffusion，另一种在慕尼黑发表的方法，[DIF1] 建立在 Jarzynski 上个千年的早期物理学工作 [DIF2] 和最近的论文的基础上。 [DIF3-5]
1991 年，我发布了另一种基于两个称为可预测性最小化的对抗性神经网络的 ML 方法，用于创建部分冗余数据的分离表示，并于 1996 年应用于图像。[PM0-2][AC20][R2][MIR]（第 7 节） )
1990 年 2 月：生成对抗网络/好奇心
生成对抗网络 (GAN) 已经变得非常流行。[MOST] 它们于 1990 年首次在慕尼黑以人工好奇心的名义发表。[AC90-20][GAN1] 两个决斗的神经网络（一个概率生成器和一个预测器）正试图 在 minimax 游戏中最大化彼此的损失。[AC]（第 1 节）生成器（称为控制器）生成概率输出（使用随机单位 [AC90]，就像在后来的 StyleGANs[GAN2] 中一样）。 预测器（称为世界模型）看到控制器的输出并预测环境对它们的反应。 使用梯度下降，预测器 NN 最小化它的错误，而生成器 NN 试图使输出最大化这个错误：一个网络的损失是另一个网络的收益。[AC90]（世界模型也可以用于连续在线行动规划。 [AC90][计划 2-3][计划])
1990-91 年以来的人工好奇心和创造力
在 2014 年一篇关于 GAN 的论文之前 4 年，[GAN1] 我著名的 2010 年调查 [AC10] 将 1990 年的生成对抗性神经网络总结如下：“神经网络作为预测世界模型用于最大化控制器的内在奖励，这 与模型的预测误差成正比”（已最小化）。
2014 年的 GAN 就是这样的一个例子，其中试验非常短（就像老虎机问题）并且环境简单地返回 1 或 0，这取决于控制器（或生成器）的输出是否在给定的集合中。[AC20][AC] [T22]（第十七节）
其他早期的对抗性机器学习设置 [S59][H90] 非常不同——它们既不涉及无监督神经网络，也不涉及建模数据，也不使用梯度下降。[AC20]
可预测性最小化：无监督极小极大博弈，其中一个神经网络最小化另一个最大化的目标函数
1990 年的原则已被广泛用于强化学习 [SIN5][OUD13][PAT17][BUR18] 和逼真图像合成 [GAN1,2] 的探索，尽管后者最近被 Rombach 等人接管。 s Latent Diffusion，另一种在慕尼黑发表的方法，[DIF1] 建立在 Jarzynski 上个千年的早期物理学工作 [DIF2] 和最近的论文的基础上。 [DIF3-5]
1991 年，我发布了另一种基于两个称为可预测性最小化的对抗性神经网络的 ML 方法，用于创建部分冗余数据的分离表示，并于 1996 年应用于图像。[PM0-2][AC20][R2][MIR]（第 7 节） )
1991 年 3 月：具有线性化自注意力的变形金刚
最近，Transformers[TR1] 风靡一时，例如生成听起来像人类的文本。[GPT3] Transformers with “linearized self-attention”[TR5-6] 发表于 1991 年 3 月[FWP0-1][FWP6] [FWP]（除了正常化——见 2022 年 30 周年推文）。 这些所谓的“Fast Weight Programmers”或“Fast Weight Controllers”[FWP0-1] 像传统计算机一样将存储和控制分开，但是以端到端可微分的、自适应的、完全神经的方式（而不是 混合时尚[PDA1-2][DNC])。 标准变形金刚 [TR1-4] 中的“自注意力”将其与投影和 softmax 相结合（使用像我在 1993 年 [ATT][FWP2][R4] 中介绍的那样的注意力术语）。
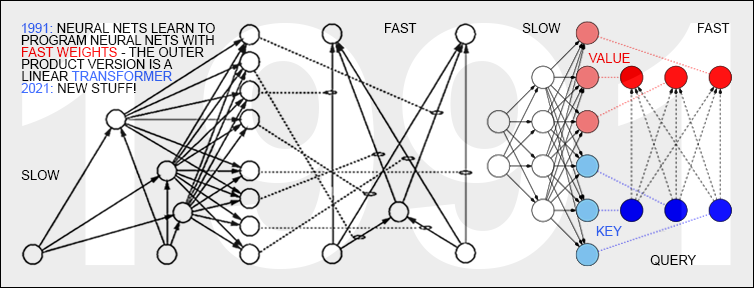1991 年 3 月 26 日：神经网络学习使用快速权重对神经网络进行编程——就像今天的 Transformer 变体一样。 2021 年：新东西！
今天的变形金刚大量使用无监督预训练[UN0-3]（见下一节），这是另一种深度学习方法，首次发表于我们 1990-1991 年的奇迹年[MIR][MOST]
1991 年的快速权重程序员还导致了元学习自参照神经网络，它们可以在自己身上运行自己的权重变化算法或学习算法，并对其进行改进，并改进它们改进它的方式，等等。 这项工作自 1992 年以来[FWPMETA1-9][HO1] 扩展了我 1987 年的毕业论文，[META1] 介绍了不仅用于学习而且用于元学习或学习学习的算法，[META] 通过经验学习更好的学习算法。 这在 2010 年代[DEC] 变得非常流行，当时计算机的速度快了一百万倍。
1991 年 4 月：通过自监督预训练进行深度学习
今天最强大的 NN 往往非常深，也就是说，它们有很多层神经元或许多后续计算阶段。[MIR] 然而，在 1990 年代之前，基于梯度的训练对深度 NN 效果不佳，仅适用于浅层 NN [DL1-2]（但请参阅 1989 年的一篇论文 [MOZ]）。 这个深度学习问题对于循环神经网络最为明显。 与人脑相似，但与更有限的前馈神经网络 (FNN) 不同，RNN 具有反馈连接。 这使得 RNN 成为功能强大的通用并行顺序计算机，可以处理任意长度的输入序列（想想语音数据或视频）。 RNN 原则上可以实现任何可以在您的笔记本电脑或任何其他现有计算机上运行的程序。 如果我们想要构建通用人工智能 (AGI)，那么它的底层计算基础必须更像 RNN 而不是 FNN，因为 FNN 从根本上是不够的； RNN 和类似系统之于 FNN 就像通用计算机之于袖珍计算器一样。 特别是，与 FNN 不同，RNN 原则上可以处理任意深度的问题。[DL1] 然而，在 1990 年代之前，RNN 在实践中未能学习深度问题。[MIR]（第 0 节）
为了通过基于 RNN 的“一般深度学习”克服这个缺点，我构建了一个自我监督的 RNN 层次结构，它在多个抽象层次和多个自组织时间尺度上学习表示：[LEC] 神经序列分块器 [UN0] 或神经网络 History Compressor.[UN1] 每个 RNN 都试图解决预测其下一个输入的借口任务，仅将意外输入（因此也是目标）发送到上面的下一个 RNN。 由此产生的压缩序列表示极大地促进了下游监督深度学习，例如序列分类。
尽管当时的计算机每一美元的计算速度比今天慢了大约一百万倍，但到 1993 年，上面的神经历史压缩器已经能够解决以前无法解决的深度 > 1000[UN2]（需要超过 1,000 个后续计算阶段）的“非常深度学习”任务 ——这样的阶段越多，学习越深入）。 1993 年，我们还发布了神经历史压缩器的连续版本。[UN3]（另请参阅最近关于无监督的基于神经网络的抽象的工作。[OBJ1-5]）
这项工作十多年后，[UN1] 发布了一种类似的用于更有限的前馈神经网络 (FNN) 的无监督方法，通过对称为深度信念网络 (DBN) 的 FNN 堆栈进行无监督预训练来促进监督学习。[UN4] 2006 年的理由基本上是我在 1990 年代初期为我的 RNN 堆栈使用的理由：每个更高级别都试图减少下面级别中数据表示的描述长度（或负对数概率）。[HIN][T22][MIR]
1991 年 4 月：将一个 NN 提炼成另一个 NN 使用我 1991 年的 NN 蒸馏程序，可以将上述神经历史压缩器的分层内部表示折叠成单个循环神经网络 (RNN)。[UN0-1][MIR] 在这里，教师神经网络的知识被“蒸馏”成 一个学生 NN，通过训练学生 NN 模仿老师 NN 的行为（同时还对学生 NN 重新训练以前学过的技能，这样它就不会忘记它们）。 NN 蒸馏也在多年后重新发表，[DIST2][MIR][HIN][T22] 并在今天被广泛使用。
如今，无监督预训练被 Transformers[TR1-6] 大量用于自然语言处理和其他领域。 值得注意的是，具有线性化自注意力的 Transformers 也首次在我们的 Annus Mirabilis of 1990-1991 中发表[FWP0-6]，[MIR][MOST] 以及用于深度学习的无监督/自监督预训练。[UN0-3 ] 见上一节。
1991 年 6 月：基本问题：梯度消失
Sepp Hochreiter 对基本深度学习问题的分析 (1991) 深度学习之所以困难，是因为我的第一个学生 Sepp Hochreiter 在他的毕业论文中于 1991 年确定并分析了基本深度学习问题，我很高兴能够监督。[VAN1] 首先 他实现了上面的神经历史压缩器，但后来做了更多：他表明深度神经网络存在现在著名的梯度消失或爆炸问题：在典型的深度或循环网络中，反向传播的误差信号要么迅速缩小，要么从中消失 界限。 在这两种情况下，学习都会失败（比较[VAN2]）。 这种分析导致了现在称为 LSTM 的基本原理（见下文）。
1991 年 6 月：LSTM / Highway Nets / ResNets 的根源
长短期记忆 (LSTM) 循环神经网络 [LSTM1-6] 克服了 Sepp 在其上述 1991 年毕业论文 [VAN1] 中确定的基本深度学习问题，我认为这是历史上最重要的文献之一 机器学习。 它还通过我们在 1995 年的一份技术报告中称为 LSTM 的基本原理（例如恒定错误流）提供了解决问题的重要见解。[LSTM0] 在 1997 年主要同行评审出版物之后 [LSTM1][25y97] （现在是 20 世纪被引用次数最多的 NN 文章 [MOST]），LSTM 及其训练程序在我在 IDSIA 的瑞士 LSTM 资助下通过我后来的学生 Felix Gers、Alex Graves 和其他人的工作得到了进一步改进。 一个里程碑是带有遗忘门 [LSTM2] 的“香草 LSTM 架构”——今天每个人都在使用的 1999-2000 的 LSTM 变体，例如在谷歌的 Tensorflow 中。 Alex 是我们首次将 LSTM 成功应用于语音（2004 年）的主要作者。[LSTM10] 2005 年首次发布了具有全时间反向传播的 LSTM 和双向 LSTM[LSTM3]（现已广泛使用）。
2006 年的另一个里程碑是用于同时比对和识别序列的训练方法“Connectionist Temporal Classification”或 CTC[CTC]。 我们的团队在 2007 年成功地将 CTC 训练的 LSTM 应用于语音 [LSTM4]（也使用分层 LSTM 堆栈 [LSTM14]）。 这导致了第一个卓越的端到端神经语音识别。 它与 20 世纪 80 年代末以来将神经网络与传统方法（如隐马尔可夫模型 (HMM)）相结合的混合方法有很大不同。[BW][BRI][BOU][HYB12][T22] 在 2009 年，通过 Alex 的努力， CTC训练的LSTM成为第一个赢得国际比赛的RNN，即三项ICDAR 2009 Connected Handwriting Competitions（法语，波斯语，阿拉伯语）。 这引起了业界的极大兴趣。 LSTM 很快被用于涉及序列数据的所有事物，例如语音 [LSTM10-11][LSTM4][DL1] 和视频。 2015 年，CTC-LSTM 组合显着改善了谷歌在 Android 智能手机上的语音识别。[GSR15] 许多其他公司采用了这一点。[DL4] 谷歌 2019 年新的设备语音识别（现在在你的手机上，而不是在服务器上） 仍然是基于LSTM。
1995：神经概率语言模型
第一个出色的端到端神经机器翻译也是基于 LSTM。 1995 年，我们已经有了一个优秀的神经概率文本模型 [SNT]，其基本概念在 2003 年 [NPM][T22] 中得到了重用——另请参阅 Pollack 早期关于词嵌入和其他结构的工作 [PO87][PO90] 以及 Nakamura 和 Shikano 1989 年的词类别预测模型。[NPMa] 2001 年，我们表明 LSTM 可以学习 HMM 等传统模型无法学习的语言，[LSTM13] 即神经“亚符号”模型突然擅长学习“符号”任务。 计算仍然必须便宜 1000 倍，但到 2016 年，谷歌翻译 [GT16]——其白皮书 [WU] 提到 LSTM 超过 50 次——基于两个连接的 LSTM，[S2S] 一个用于传入文本，一个用于传出翻译 - 比以前好得多。[DL4] 到 2017 年，LSTM 还支持 Facebook 的机器翻译（每周超过 300 亿次翻译——最受欢迎的 YouTube 视频需要数年时间才能实现仅 100 亿次点击），[FB17][DL4] 苹果的 大约 10 亿部 iPhone 上的 Quicktype，[DL4] 亚马逊 Alexa 的声音，[DL4] 谷歌的图像标题生成 [DL4] 和自动电子邮件回复 [DL4] 等。《商业周刊》称 LSTM “可以说是最商业化的 AI 成就”。[AV1 ] 到 2016 年，谷歌数据中心超过四分之一的强大推理计算能力用于 LSTM（5% 用于另一种流行的深度学习技术，称为 CNN——见上文）。[JOU17] 当然，我们的 LSTM 也是 大量用于医疗保健和医疗诊断——一个简单的谷歌 e Scholar search 出现了无数标题中带有“LSTM”的医学文章。[DEC]
通过我的学生 Rupesh Kumar Srivastava 和 Klaus Greff 的工作，LSTM 原理也促成了我们 2015 年 5 月的 Highway Network[HW1]，这是第一个具有数百层的非常深的 FNN（以前的 NN 最多只有几十层） ). Microsoft 的 ResNet[HW2]（赢得了 ImageNet 2015 竞赛）是其一个版本（ResNet 是大门始终敞开的 Highway Net）。 早期的 Highway Nets 在 ImageNet 上的表现与它们的 ResNet 版本大致相同。[HW3] highway gates 的变体也用于某些算法任务，其中纯残差层不能很好地工作。[NDR]
LSTM / Highway Net 原理是现代深度学习的核心
深度学习完全是关于神经网络深度的。[DL1] 在 1990 年代，LSTM 为受监督的循环神经网络带来了本质上无限的深度； 在 2000 年代，受 LSTM 启发的 Highway Nets 将其引入前馈神经网络。 LSTM 已成为 20 世纪引用最多的神经网络； 名为 ResNet 的 Highway Net 版本是 21 世纪引用最多的神经网络。[MOST]（然而，引用是衡量真实影响的一个非常值得怀疑的衡量标准。[NAT1]）
1980s-：在没有老师的情况下学习行动的神经网络 前面的部分主要关注用于被动模式识别/分类的深度学习。 然而，NN 也与强化学习 (RL)、[KAE96][BER96][TD3][UNI][GM3][LSTMPG] 最通用的学习类型相关。 一般的 RL 智能体必须在没有教师帮助的情况下发现如何与动态的、最初未知的、部分可观察的环境进行交互，以最大化其预期的累积奖励信号。[DL1] 动作之间可能存在任意的、先验未知的延迟 和可察觉的后果。 RL 问题与计算机科学的任何问题一样困难，因为任何具有可计算描述的任务都可以在通用 RL 框架中制定。[UNI]
某些强化学习问题可以通过 80 年代之前发明的非神经技术来解决：蒙特卡洛（树）搜索（MC，1949 年）、[MOC1-5] 动态规划（DP，1953 年）、[BEL53] 人工进化（1954 年） ,EVO1-7 alpha-beta-pruning (1959),[S59] 控制理论与系统辨识 (1950s),[KAL59][GLA85] 随机梯度下降 (SGD, 1951),[ STO51-52]和通用搜索技术（1973）。[AIT7]
然而，深度 FNN 和 RNN 是改进某些类型的 RL 的有用工具。 在 1980 年代，函数逼近和 NN 的概念与系统识别相结合，[WER87-89][MUN87][NGU89] DP 及其在线变体 Temporal Differences (TD)，[TD1-3] 人工进化，[EVONN1- 3] 和策略梯度。[GD1][PG1-3] 可以在第 1 节中找到有关此的许多其他参考资料。 2015 年调查的 6 [DL1]
当环境存在马尔可夫接口 [PLAN3]，使得 RL 机器的当前输入传达了确定下一个最佳动作所需的所有信息时，基于 DP/TD/MC 的 FNN 的 RL 可以非常成功，如图所示 1994 年 [TD2]（大师级西洋双陆棋玩家）和 2010 年代 [DM1-2a]（围棋、国际象棋和其他游戏的超人玩家）。
对于没有马尔可夫接口的更复杂的情况，学习机不仅要考虑当前输入，还要考虑以前输入的历史，我们的 RL 算法和 LSTM[LSTM-RL][RPG] 的组合已经成为标准，特别是， 我们的 LSTM 通过策略梯度训练 (2007).[RPG07][RPG][LSTMPG]
例如，2018 年，PG 训练的 LSTM 是 OpenAI 著名的 Dactyl 的核心，它学会了在没有老师的情况下控制灵巧的机器人手。[OAI1][OAI1a] 视频游戏类似：2019 年，DeepMind（由 我实验室的一名学生）在星际争霸游戏中击败了一名职业玩家，这在理论上比国际象棋或围棋 [DM2] 在许多方面都更难，使用的是 Alphastar，其大脑具有由 PG 训练的深层 LSTM 核心。[DM3] 强化学习 LSTM（占模型总参数数的 84%）也是著名的 OpenAI Five 的核心，它学会了在 Dota 2 视频游戏（2018 年）中击败人类专家。[OAI2] 比尔·盖茨称这是“进步的巨大里程碑” 人工智能”。[OAI2a][MIR]（第 4 节）[LSTMPG]
RL 的未来将是关于使用复杂输入流的紧凑时空抽象进行学习/组合/规划——关于常识推理[MAR15] 和学习思考。[PLAN4-5] 分层方式，在多个抽象级别和多个时间尺度？[LEC] 我们在 1990-91 年发表了这些问题的答案：自我监督的神经历史压缩器 [UN][UN0-3] learn to represent percepts at multiple levels 抽象和多个时间尺度（见上文），而端到端可区分的基于神经网络的子目标生成器[HRL3] [MIR]（第 10 节）通过梯度下降学习分层行动计划（见上文）。 更复杂的学习抽象思考的方法发表于 1997[AC97][AC99][AC02] 和 2015-18.[PLAN4-5]
是硬件，笨蛋！
如果没有不断改进和加速计算机硬件，深度学习算法在过去千年中的最新突破（见前几节）是不可能的。 如果不提及这种已经运行了至少两千年的进化，任何人工智能和深度学习的历史都是不完整的。
第一个已知的基于齿轮的计算设备是 2000 多年前古希腊的 Antikythera 机制（一种天文钟）。
也许世界上第一台实用的可编程机器是 1 世纪 [SHA7a][RAU1] 由亚历山大的赫伦制造的自动剧院（显然他还拥有第一台已知的工作蒸汽机 - Aeolipile）。
Banu Musa 兄弟在 9 世纪在巴格达制造的音乐自动机可能是第一台具有存储程序的机器。[BAN][KOE1] 它使用旋转圆柱体上的销来存储控制蒸汽驱动长笛的程序——比较 Al-Jazari 的可编程 1206.[SHA7b] 的鼓机
1600 年代带来了更灵活的机器，可以根据输入数据计算答案。 第一个用于简单算术的基于数据处理齿轮的专用计算器是由 Wilhelm Schickard 于 1623 年建造的，Wilhelm Schickard 是“自动计算之父”称号的候选人之一，其次是 Blaise Pascal 的高级 Pascaline（1642 年）。 1673 年，已经提到的戈特弗里德·威廉·莱布尼茨（被称为“有史以来最聪明的人”[SMO13]）设计了第一台可以执行所有四种算术运算的机器（计步器），并且是第一台带有记忆的机器。[BL16] 他还描述了由穿孔卡 (1679)、[L79][L03][LA14][HO66] 控制的二进制计算机的原理，并发表了链式法则[LEI07-10]（见上文），深度学习和现代的基本要素 人工智能。
大约 1800 年，约瑟夫-玛丽·雅卡尔 (Joseph-Marie Jacquard) 和其他人在法国制造了第一台商业程序控制机器（基于打孔卡的织机）——他们可能是编写世界上第一个工业软件的第一批“现代”程序员。 他们启发了 Ada Lovelace 和她的导师 Charles Babbage（英国，大约 1840 年）。 他计划但无法构建一台可编程的通用计算机（只有他的非通用专用计算器导致了 20 世纪的工作复制品）。
Leonardo Torres y Quevedo，20 世纪第一个实用 AI 的先驱 1914 年，西班牙人 Leonardo Torres y Quevedo（在介绍中提到）成为 20 世纪第一个 AI 先驱，他创造了第一个工作的国际象棋终端玩家（当时国际象棋被认为 作为一种仅限于智能生物领域的活动）。 几十年后，当另一位 AI 先驱 Norbert Wiener [WI48] 在 1951 年巴黎 AI 会议上与它对战时，这台机器仍然被认为令人印象深刻。 [AI51][BRO21][BRU4]
1935 年至 1941 年间，Konrad Zuse 创造了世界上第一台可运行的可编程通用计算机：Z3。 1936 年的相应专利 [ZU36-38][RO98][ZUS21] 描述了可编程物理硬件所需的数字电路，早于克劳德香农 1937 年关于数字电路设计的论文。[SHA37] 与巴贝奇不同，Zuse 使用了莱布尼茨的二进制计算原理 (1679)[L79][LA14][HO66][L03] 代替传统的十进制计算。 这极大地简化了硬件。[LEI21,a,b] 忽略任何物理计算机不可避免的存储限制，Z3 的物理硬件在哥德尔 [GOD][GOD34, GOD34, 21,21a] (1931-34)、Church[CHU] (1935)、Turing[TUR] (1936) 和 Post[POS] (1936)。 简单的算术技巧可以弥补 Z3 缺少明确的条件跳转指令。[RO98] 今天，大多数计算机都像 Z3 一样是二进制的。
Z3 使用带有明显移动开关的电磁继电器。 第一个电子专用计算器（其运动部件是电子，太小以至于看不见）是约翰·阿塔纳索夫（“管基计算之父”[NASC6a]）的二进制 ABC（美国，1942 年）。 与 1600 年代基于齿轮的机器不同，ABC 使用真空管——今天的机器使用 Julius Edgar Lilienfeld 于 1925 年获得专利的晶体管原理。[LIL1-2] 但与 Zuse 的 Z3 不同，ABC 不能自由编程。 Tommy Flowers（英国，1943-45 年）的电子巨像机器也没有用来破解纳粹密码。[NASC6]
由 Zuse (1941)[RO98] 以外的人建造的第一台通用工作可编程机器是 Howard Aiken 的十进制 MARK I（美国，1944 年）。 由 Eckert 和 Mauchly (1945/46) 开发的速度快得多的十进制 ENIAC 是通过重新布线来编程的。 数据和程序都被“曼彻斯特宝贝”（Williams, Kilburn & Tootill, UK, 1948）和 1948 年升级的 ENIAC 存储在电子存储器中，通过将数字指令代码输入只读存储器来重新编程。 [HAI14b]
从那时起，计算机通过集成电路 (IC) 变得更快。 1949 年，西门子的 Werner Jacobi 为在公共基板上具有多个晶体管的 IC 半导体申请了专利（于 1952 年授予）。[IC49-14] 1958 年，Jack Kilby 展示了带有外部导线的 IC。 1959 年，罗伯特·诺伊斯 (Robert Noyce) 提出了单片 IC。[IC14] 自 1970 年代以来，图形处理单元 (GPU) 已被用于通过并行处理来加速计算。 今天（2022 年）的 IC/GPU 包含数十亿个晶体管（几乎所有晶体管都是 Lilienfeld 的 1925 FET 类型[LIL1-2]）。
1941 年，Zuse 的 Z3 每秒可以执行大约一个基本运算（例如加法）。 从那时起，每 5 年，计算成本就会降低 10 倍（请注意，他的定律比摩尔定律要古老得多，摩尔定律指出每个芯片的晶体管 [LIL1-2] 数量每 18 个月翻一番）。 截至 2021 年，即 Z3 之后的 80 年，现代计算机每秒可以以相同（经通货膨胀调整后）的价格执行约 1000 万亿条指令。 对这种指数趋势的天真推断预测，21 世纪将出现廉价计算机，其原始计算能力是所有人类大脑总和的一千倍。[RAW]
物理极限在哪里？ 根据 Bremermann (1982)，[BRE] 一台质量为 1 千克和体积为 1 升的计算机最多可以在最多 1032 位上每秒执行最多 1051 次操作。 上述趋势将在 Z3 之后大约 25 年，即 2200 年左右达到布雷默曼极限。但是，由于太阳系中只有 2 x 1030 千克的质量，因此趋势势必会在几个世纪内打破，因为光速 将极大地限制额外质量的获取，例如，以其他太阳系的形式，通过及时的函数多项式，如先前在 2004 年指出的那样。[OOPS2][ZUS21]
物理学似乎要求未来高效的计算硬件必须像大脑一样，在 3 维空间中有许多紧凑放置的处理器，由许多短线和少量长线稀疏地连接，以最小化总连接成本（即使“线” 实际上是光束）。[DL2] 基本架构本质上是一种深度的、稀疏连接的 3 维 RNN，这种 RNN 的深度学习方法有望变得比今天更加重要。[DL2 ]
不要忽视 1931 年以来的人工智能理论
现代人工智能和深度学习的核心主要基于近几个世纪的简单数学：微积分/线性代数/统计学。 然而，要在上一节中提到的现代硬件上有效地实现这个核心，并为数十亿人推出它，需要大量的软件工程，基于上个世纪发明的大量智能算法。 这里没有余地一一提及。 然而，至少我会列出人工智能和计算机科学理论的一些最重要的亮点。
1930 年代初期，哥德尔创立了现代理论计算机科学。[GOD][GOD34][LEI21,21a] 他介绍了一种通用编码语言 (1931-34)。[GOD][GOD34-21a] 它基于整数， 并允许以公理形式形式化任何数字计算机的操作。 哥德尔用它来表示数据（例如公理和定理）和程序 [VAR13]（例如数据操作的证明生成序列）。 他著名地构造了关于其他形式陈述的计算的形式陈述——特别是暗示它们不可判定的自引用陈述，给定一个计算定理证明器，系统地从一组可枚举的公理中列举所有可能的定理。 因此，他确定了算法定理证明、计算和任何类型的基于计算的 AI 的基本限制。[GOD][BIB3][MIR]（第 18 节）[GOD21,21a]
像大多数伟大的科学家一样，哥德尔建立在早期工作的基础上。 他将 Georg Cantor 的对角化技巧 [CAN]（在 1891 年表明存在不同类型的无穷大）与 Gottlob Frege [FRE]（他在 1879 年引入了第一种形式语言）、Thoralf Skolem [SKO23]（他 在 1923 年引入了原始递归函数）和 Jacques Herbrand [GOD86]（他发现了 Skolem 方法的局限性）。 这些作者又建立在 Gottfried Wilhelm Leibniz[L86][WI48]（见上文）的正式思想代数（1686 年）的基础上，它与后来的 1847 年布尔代数演绎等价[LE18]。[BOO]
1935 年，Alonzo Church 通过证明 Hilbert & Ackermann 的 Entscheidungsproblem（决策问题）没有一般解决方案，得出了哥德尔结果的推论/扩展。[CHU] 为此，他使用了他的替代通用编码语言，称为 Untyped Lambda Calculus， 它构成了极具影响力的编程语言 LISP 的基础。 1936年，Alan M. Turing引入了另一个通用模型：图灵机。[TUR]他重新推导了上述结果。[CHU][TUR][HIN][GOD21,21a][TUR21][LEI21,21a] 在 1936 年的同一年，Emil Post 发表了另一个独立的通用计算模型。[POS] 今天我们知道很多这样的模型。
Konrad Zuse 不仅创造了世界上第一台可工作的可编程通用计算机，[ZU36-38][RO98][ZUS21]，他还设计了第一种高级编程语言 Plankalkül。[BAU][KNU]，他将其应用于国际象棋 在 1945 年 [KNU] 和 1948 年的定理证明。[ZU48] 比较 Newell 和 Simon 在定理证明方面的后期工作（1956）。[NS56] 1940 年代至 70 年代的许多早期人工智能实际上是关于哥德尔风格的定理证明和演绎 [GOD][GOD34,21,21a] 通过专家系统和逻辑编程。
1964 年，Ray Solomonoff 将贝叶斯（实际上是拉普拉斯[STI83-85]）概率推理与理论计算机科学[GOD][CHU][TUR][POS] 相结合，推导出一种数学上最优（但计算上不可行）的学习预测未来的方式 [AIT1][AIT10] 与 Andrej Kolmogorov 一起创立了 Kolmogorov 复杂性理论或算法信息论 (AIT)，[AIT1-22] 通过形式化概念超越了传统信息论 [SHA48][KUL] 奥卡姆剃刀原理，通过计算数据的最短程序的概念，支持对给定数据进行最简单的解释。 这个概念有许多可计算的、有时间限制的版本，[AIT7][AIT5][AIT12-13][AIT16-17] 以及神经网络的应用。[KO2][CO1-3]
在 2000 年代初期，Marcus Hutter（在我的瑞士国家科学基金会资助 [UNI] 下工作时）通过最佳动作选择器（通用 AI）增强了 Solomonoff 的通用预测器 [AIT1][AIT10]，用于强化学习代理，这些代理最初未知（ 但至少是可计算的）环境。[AIT20,22] 他还推导出了所有明确定义的计算问题的渐近最快算法，[AIT21] 解决任何问题的速度与此类问题的未知最快求解器一样快，除了加法常数 不依赖于问题的大小。
自参考 2003 哥德尔机 [GM3-9] 的更一般的最优性不限于渐近最优性。
然而，由于各种原因，这种数学上最优的 AI 在实践中尚不可行。 相反，实用的现代 AI 是基于次优的、有限的，但还不是很容易理解的技术，例如神经网络和深度学习，这是本文的重点。 但谁知道 20 年后会出现什么样的 AI 历史呢？
从大爆炸到遥远的未来的更广泛的历史背景
信用分配是关于在历史数据中寻找模式，并弄清楚以前的事件是如何促成某些事件的。 历史学家这样做。 物理学家这样做。 AI 也会这样做。 让我们退后一步，在最广泛的历史背景下审视人工智能：自大爆炸以来的所有时间。 2014 年，我在其中发现了一个美丽的指数加速模式，[OMG] 从那以后我在许多演讲中都提出了它，它也被写进了 Sibylle Berg 的获奖书籍“GRM：Brainfuck”。[OMG2] 以前出版 这种模式跨越的时间间隔要短得多：只有几十年或几个世纪或最多几千年。[OMG1]
事实证明，从人类的角度来看，自宇宙诞生以来最重要的事件都整齐地排列在指数加速的时间轴上（误差线大多低于 10%）。 事实上，历史似乎在 2040 年左右汇聚在一个欧米茄点。 我喜欢叫它Omega，因为一个世纪前，Teilhard de Chardin称Omega是人类将达到下一个层次的点。[OMG0]另外，Omega听起来比“Singularity”[SING1-2]好听多了——听起来有点 就像“哦，我的上帝。”[OMG]
让我们从138亿年前的大爆炸说起。 我们将这个时间除以 4 得到大约 35 亿年。 欧米茄是2040年左右。 在欧米茄负 35 亿年时，发生了一件非常重要的事情：生命出现在这个星球上。
我们再次花费四分之一的时间。 我们在 9 亿年前出现，当时发生了一件非常重要的事情：类似动物的移动生命出现了。
我们再除以 4。我们在 2.2 亿年前，当哺乳动物被发明时，我们就出来了，我们的祖先。
我们再次除以 4。5500 万年前，第一批灵长类动物出现了，我们的祖先。
自宇宙诞生以来最重要的事件似乎整齐地排列在 2040 年左右收敛于 Omega 点的指数加速时间线上（J Schmidhuber，2014 年）
我们再次除以 4。1300 万年前，第一批原始人出现了，我们的祖先。 我不知道为什么所有这些除以 4 的除法总是在历史上出现这些决定性的时刻。 但他们确实如此。 我也试过三度、五度和谐波比例，但似乎只有四分之一奏效。
我们再次除以 4。350 万年前发生了一件非常重要的事情：技术的黎明，正如大自然所说：第一批石器。
我们除以 4。80 万年前，下一个伟大的技术突破发生了：可控火力。
我们除以 4。 20 万年前，解剖学上的现代人变得突出，我们的祖先。
我们除以 4. 5 万年前，出现了行为上现代的人，我们的祖先，并开始在世界上殖民。
我们再次除以 4。我们在 13000 年前出现，当时发生了一件非常重要的事情：动物的驯化、农业、第一批定居点——文明的开始。 现在我们看到，所有的文明只是世界历史上的一瞬间，只是大爆炸以来时间的百万分之一。 农业和航天器几乎是同时发明的。
我们除以 4。 3300 年前，铁器时代出现了第一次人口爆炸。
我们除以 4。请记住，收敛点 Omega 是 2040 年左右。 欧米茄负 800 年——那是在 13 世纪，在中国，铁和火以枪炮、大炮和火箭的形式结合在一起。 从那时起，这就定义了世界，西方仍然远远落后于欠中国的许可费。
我们再次除以 4。 欧米茄减去 200 年——我们来到了 19 世纪中叶，当时铁和火以越来越复杂的形式结合在一起，通过改进的蒸汽机为工业革命提供动力，基于博蒙特、帕潘、纽科门的工作 、瓦特和其他人（1600 年代至 1700 年代，超越了 1 世纪亚历山大港的 Heron [RAU1] 的第一台简单蒸汽机）。 电话（例如 Meucci 1857、Reis 1860、Bell 1876）[NASC3] 开始彻底改变通信方式。 疾病的细菌理论（巴斯德和科赫，1800 年代后期）彻底改变了医疗保健并使人们的平均寿命更长。 大约在 1850 年，以化肥为基础的农业革命（Sprengel & von Liebig，1800 年代初期）帮助引发了第二次人口爆炸，并在 20 世纪达到顶峰，当时世界人口翻了两番，让 20 世纪在所有世纪中脱颖而出 人类的历史，由制造人造肥料的 Haber-Bosch 工艺驱动，如果没有人造肥料，世界最多只能养活 40 亿人。[HAB1-2]
我们再除以 4。 欧米茄减去 50 年——差不多是 1990 年，20 世纪 3 场大战的结束：第一次世界大战、第二次世界大战和冷战。 最有价值的 7 家上市公司都是日本公司（如今大多数都在美国）； 然而，中国和美国西海岸都开始迅速崛起，为 21 世纪奠定了基础。 通过手机和无线革命（基于 1800 年代发现的无线电波）以及面向所有人的廉价个人电脑，数字神经系统开始席卷全球。 WWW 是由 Tim Berners-Lee 在瑞士的欧洲粒子对撞机上创建的。 现代人工智能也大约在这个时候开始：第一辆真正的自动驾驶汽车于 1980 年代由 Ernst Dickmanns 团队在慕尼黑制造（到 1994 年，他们的机器人汽车以最高 180 公里/小时的速度在高速公路上行驶）。 [AUT] 那时候，我在写我 1987 年的毕业论文 [META1]，它介绍了不仅用于学习而且用于元学习或学习学习的算法，[META] 通过经验学习更好的学习算法（现在很流行 主题 [DEC])。 然后是我们在 TU Munich 的奇迹年 1990-91[MIR]，这是当今被引用最多的神经网络 [MOST] 和通过自我监督/无监督学习（见上文）进行现代深度学习的根源，[UN][UN0-3 ] LSTM/Highway Net/ResNet 原理（现在放在你智能手机的口袋里——见上文），[DL4][DEC][MOST] 人工好奇心和针对发明自己问题的代理的生成对抗性神经网络（见上文），[ AC90-AC20][PP-PP2][SA17] 具有线性化自注意力的变压器（见上文），[FWP0-6][TR5-6] 将教师 NN 提取为学生 NN（见上文），[UN][UN0- 3] 在多个抽象层次和多个时间尺度上学习行动计划（见上文），[HRL0-2][LEC] 和其他令人兴奋的东西。 其中大部分已经变得非常流行，并改善了数十亿人的生活。[DL4][DEC][MOST]
我们再次除以 4。Omega 减去 13 年——这是不久的将来的一个时间点，大约在 2030 年，届时许多人预测廉价的 AI 将具有人类的脑力。 然后是最后 13 年左右，直到 Omega，那时不可思议的事情将会发生（尽管对这一切持保留态度 [OMG1]）。
但当然，时间不会因欧米茄而停止。 也许只有人类主导的历史才会结束。 在 Omega 之后，许多好奇的元学习 AI 发明了自己的目标（这些目标已经在我的实验室中存在了几十年[AC][AC90,AC90b]）将迅速改进自己，仅受限于可计算性和物理学的基本限制。
超级智能人工智能会做什么？ 太空对人类充满敌意，但对设计合理的机器人友好，它提供的资源比我们的生物圈薄膜要多得多，后者吸收的太阳能量不到太阳能的十亿分之一。 虽然一些好奇的 AI 会继续对生命着迷，至少只要他们还没有完全理解生命，[ACM16][FA15][SP16][SA17] 大多数人会对机器人和软件生命的令人难以置信的新机会更感兴趣 在太空中。 通过小行星带及更远地区无数的自我复制机器人工厂，它们将改造太阳系，然后在几十万年内改造整个银河系，并在数百亿年内改造可及宇宙的其余部分。 尽管存在光速限制，但不断扩大的 AI 领域将有足够的时间来殖民和塑造整个可见宇宙。
让我稍微扩展一下你的想法。 宇宙还很年轻，只有 138 亿岁。 还记得我们一直除以 4 吗？ 现在让我们乘以 4！ 让我们展望未来，宇宙的年龄将是现在的 4 倍：大约 550 亿年。 届时，可见的宇宙将充满智慧。 因为在 Omega 之后，大多数 AI 将不得不去大多数物理资源所在的地方，以制造更多更大的 AI。 那些没有的不会有影响。[ACM16][FA15][SP16]
